一、什么是数据挖掘应用
成功的应用=算法(20%)+建模(40%)+数据质量(40%)
- 数据质量对项目成功是有相当大的决定作用的,好的数据质量甚至不需要用什么复杂算法就能得到很好的结果。
- 建模,通俗说,就是将数据适配成算法可以处理的格式,是连接算法和数据的桥梁,是主要的业务工作,需要正确的建模方向才有可能得到成功的结果。
- 算法,涉及数学和计算机等知识。
二、 什么是相似度
- 针对同一事件的所有新闻比较相似。
- 两个用户的收视习惯比较相似。
- 模糊查询时,查询字符串与被查询到的内容,比较相似。
- 这里“比较相似”就指的是相似度比较高,相似指的是模糊的概念,并不是完全相等。
三、 相似度计算的简单说明
- 针对同一事件的所有新闻比较相似。 将新闻分词,简单来说(仅仅是简单描述,事实上新闻相似度的算法处理有很多需要值得研究的细节),两篇新闻同时包含的词较多,那么这两篇新闻相似度相对就较高。
- 两个用户的收视习惯比较相似。 两个用户都收看了的视频较多,那么这两个用户的收视习惯相似度较高。
- 模糊查询时,查询字符串与被查询到的内容,比较相似。 如两个字符串相同的字的个数较多,字的顺序也较为一致,那么这两个字符串的相似度较高。
四、 相似度计算方法的规范化
- 确定要比较的两个实体(实体可以是新闻、收视用户、字符串等)。
- 根据业务目标,结合业务经验,提取出实体的特征(比如新闻分词,用户收视的视频、字符串中包含的字),这些特征集合就是特征向量。
- 对要比较的两个实体的特征向量进行计算,用算法计算出相似度。
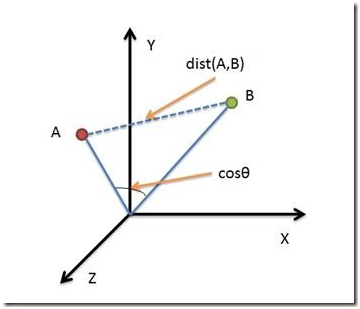
五、 相似度是向量间的距离
欧式距离
-
二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离
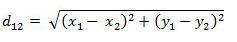
-
三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离
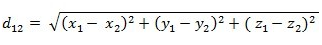
-
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离
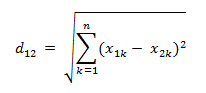
余弦距离
-
二维平面上两点a(x1,y1)与b(x2,y2)间的余弦距离,其中分母表示两个向量b和c的长度,分子表示两个向量的内积。
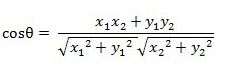
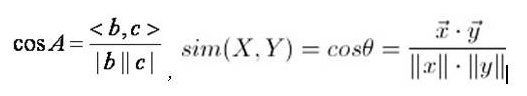
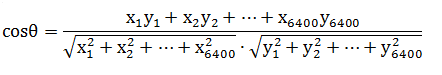
-
举一个具体的例子,假如新闻X和新闻Y对应向量分别是: x1, x2, ..., x6400和 y1, y2, ..., y6400
当两条新闻向量夹角余弦等于1时,这两条新闻完全重复(用这个办法可以删除爬虫所收集网页中的重复网页);当夹角的余弦值接近于1时,两条新闻相似(可以用作文本分类);夹角的余弦越小,两条新闻越不相关。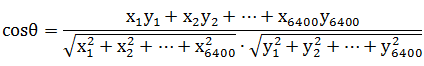
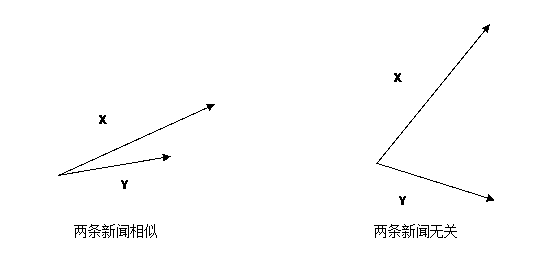
余弦距离和欧氏距离的对比
六、 实例
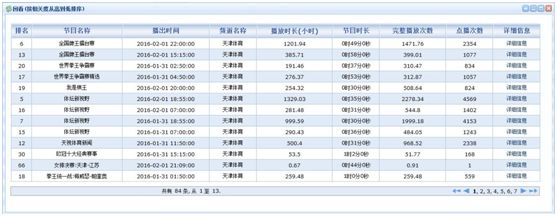
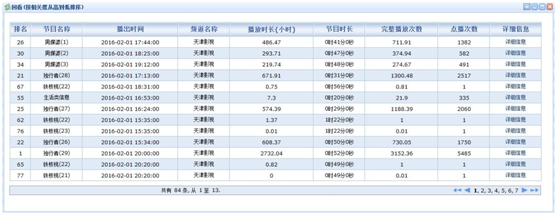
1、根据直播节目名称查询对应的回看节目
2、版权剧下线操作中遇到的片名匹配问题
-



<<疯丫头>>第1季,字符为:<<,疯,丫,头,>>,第,1,季 疯丫头第一季,字符为:疯,丫,头,第,一,季
距离为:5/ sqrt(8)* sqrt(6) =2.449*2.828=0.722
3、推荐系统中相似度问题
-
用户1,视频1,视频2,视频3,视频4
用户2,视频2,视频3,视频5,视频6
用户3,视频2,视频3,视频5,视频6,视频7
-
用户1和用户2的相似度2/sqrt(4)* sqrt(4)=0.5
用户1和用户3的相似度2/sqrt(4)* sqrt(5)=2/2.472=0.447